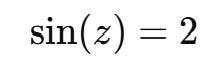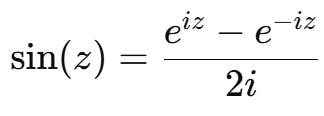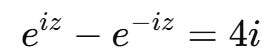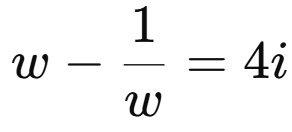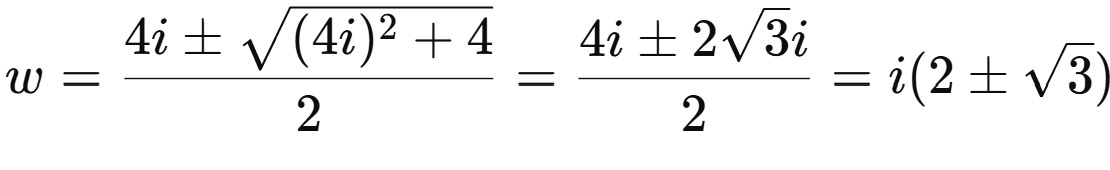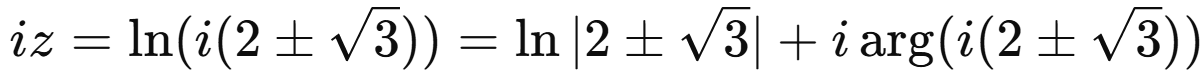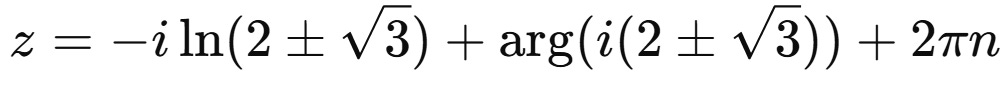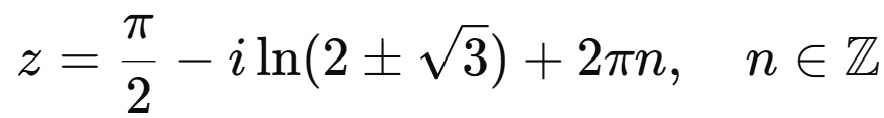A Truly Complex Equation
Can you solve this?
At first glance, this one seems impossible.
Literally.
If you’ve spent any time around trigonometry, you know sine doesn’t go above 1. So when you see the equation
sin(z) = 2
your instincts probably tell you: nope — not happening.
But that’s only true if you’re thinking real numbers. The moment you step into the complex plane, the rules change.
Wildly.
In this post, we’ll explore what it actually means to solve this “impossible” equation. We’ll dust off the definition of sine for complex inputs, break out a few exponential identities, and even peek at a contour plot of sin(z)just to see how far the rabbit hole goes.
It’s one of those problems that starts with a contradiction… and ends with a satisfying “aha.”
So if you’re ready to bend the rules a little?
Let’s dive in.
Solution
We begin with the basic observation that
has no solution for real z because
But in the complex world, sine behaves quite differently.
Let’s recall the identity for complex sine, which is
Now our attention turns to solving this expression instead.
We first multiply both sides by 2i
Here we make a clever substitution w = e^(iz)
Now multiply both sides by w, resulting in the following quadratic equation
Using the quadratic formula, we get
Notice that we are not solving for w but z instead. Therefore, we have
Taking the natural logarithm, that gives
And so z is
The 2πn term is thanks to to the periodicity of the sine function. If you want to tidy our solution one more step, we write out the argument of the second term.
And that’s the full set of complex solutions to sin(z) = 2.
If you or anyone you know want to have online math lessons, please check out my tutoring site here. Thank you!
Barry - Maths tutor in Coventry - 40£/h - 2 reviews
40£/h : I offer tutoring in the following: GCSE Maths & Further Maths (All Exam Boards) A Level Maths & Further Maths…www.superprof.co.uk
Thank you so much for reading Math Games today, whether you are a math fan, an engineer, a lecturer, a banker, a scientist, or simply some curious soul who stumbled upon this article, I am happy that you stayed till the end. If you enjoyed this algebra puzzle and believe in math education, please consider supporting here 🪙.