Are You Smart Enough To Solve This Pancake Probability Puzzle?
3 pancakes
I have noticed that for similar math puzzles, using a clickbait or attention grabbing title tends to drive up the views for the blog posts. So please don’t mind me doing that as I hope to grow the readership more.
Now this is one of those puzzles you can do in your head. And also a very good one to ask students who are learning probability.
As usual, grab your pen and paper and give this a go. When you are ready, keep reading for the solution.
Solution
We are given that the top side of the pancake is burned. Notice it doesn’t say one side, but rather top side.
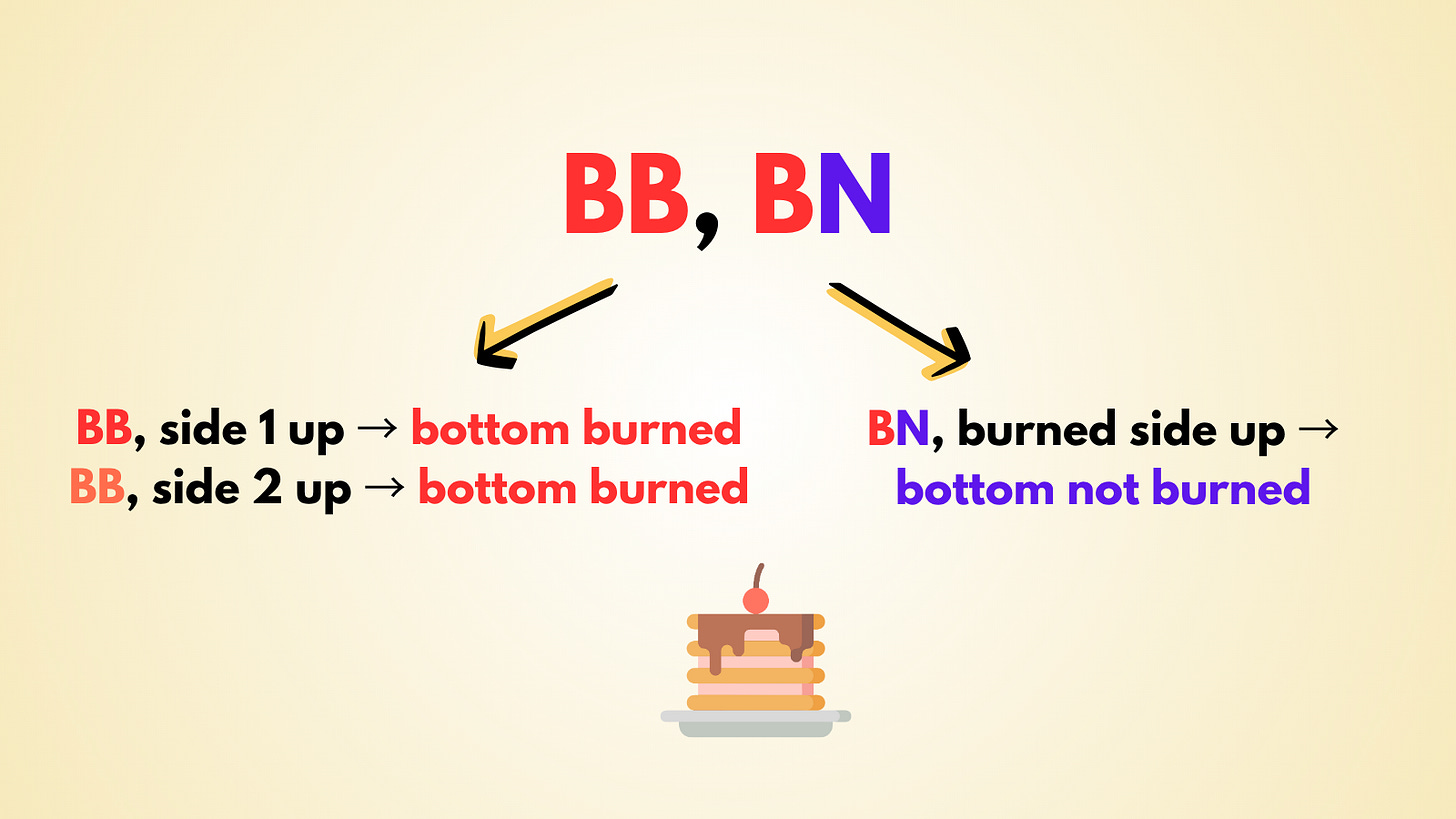
Let’s first label the pancakes.
BB means the pancake is burned on both sides.
BN means only one side is burned.
NN means both sides are not burned.
So we pick a pancake uniformly and observe that the top side is burned. This must mean we never picked the NN pancake as otherwise we wouldn’t see a burned top side at all.
So there are 3 possible scenarios where the top side is burned, and only 2 of those have the other side burned as well.
Now try the bonus puzzle below!
Five Pancakes Puzzle 🥞
You have five pancakes on a griddle.
Two pancakes have both sides burned (BB). Two pancakes have exactly one side burned (BN). One pancake is perfectly cooked on both sides (NN).
You close your eyes, stir the pancakes around, then pick one at random and place it on your plate. Without looking at which pancake it is, you lift the top side and see that it’s not burned.
What is the probability that the bottom side of your pancake is burned?
Next, suppose you flip it over and cook the bottom side once more, so that if it was unburned it now becomes burned. You then cover it again, stir the remaining pancakes, pick one at random, and look at its top side, again it’s not burned. What is now the probability that the pancake you first picked (the one you cooked a second time) has both sides burned at the end?
If you or anyone you know want to have online math lessons, please check out my tutoring site here. Thank you!
Barry — Online Maths tutor
40£/h : I offer tutoring in the following: GCSE Maths & Further Maths (All Exam Boards) A Level Maths & Further Maths…www.superprof.co.uk
Thank you so much for reading Math Games today, whether you are a math fan, an engineer, a lecturer, a banker, a scientist, or simply some curious soul who stumbled upon this article, I am happy that you stayed till the end. If you enjoyed this algebra puzzle and believe in math education, please consider supporting here 🪙. It would help out my life and this blog a lot. Thanks!