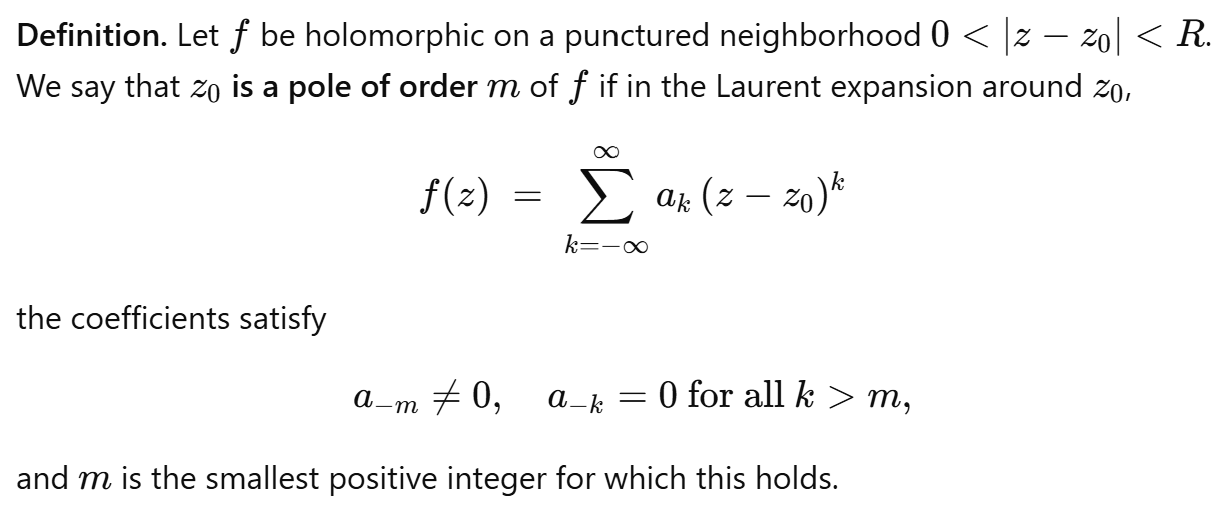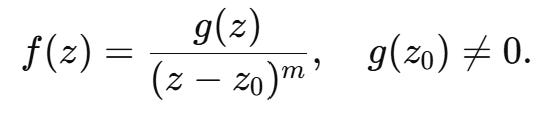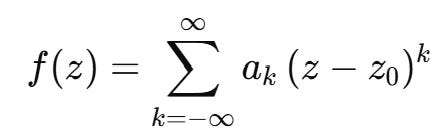Simpson Math Joke: Why Did The Mathematician Name His Dog Cauchy? Because he left a residue at every pole!

Do you know what it means?

I remember stumbling upon the Cauchy-Schwartz inequality during my first real analysis lectures at university. It was one of those fundamental inequalities about vectors that are useful in proving subsequent lemmas and theorems. You know sequences and series and upper bounds and whatnot.

It was ok, but I wouldn’t say it was anything that interesting or ‘elegant’ as some mathematicians always like to say.

So as you might have guessed now, this Simpson math joke has something to do with real analysis.

In fact, it’s more than that! It’s a play on words on complex analysis, which is what I learnt during my second year at university.

---

As one of the founders of rigorous analysis, Augustin-Louis Cauchy was born in Paris to a family of engineers and entered the École Polytechnique at age sixteen. Early in his career he taught at the École’s artillery school before holding chairs at the University of Paris and École Polytechnique. Cauchy championed a level of rigor previously unseen, insisting that every theorem rest on clear definitions and airtight proofs.

In complex analysis, his 1814 Cauchy integral theorem established that the contour integral of a holomorphic function around any closed path is zero. Building on this, he introduced the concept of residues, which were coefficients capturing a function’s behavior near singularities and formulated the residue theorem, a powerful tool for evaluating integrals. He also derived the Cauchy–Riemann equations, which characterize when a function of a complex variable is differentiable. Beyond complex analysis, Cauchy’s ε–δ definition of continuity and his convergence criteria for series laid the groundwork for modern real analysis.

Anyway, enough of his background. I doubt anyone knows him personally beyond his mathematical feats. He has already died twice as the last person who knew him personally has also died.

---

Let’s unpack the math joke here.

Why Did The Mathematician Name His Dog Cauchy? Because he left a residue at every pole!

You might be thinking, what exactly are ‘poles’ and ‘residues’?

In brief, poles are singularities of a function, and residues are the coefficients you pick up when you expand around those singularities.

Definition of a Pole

A pole of a function f(z) at a point z0 is a particular type of isolated singularity where f “blows up” in a controlled, algebraic way.

Formal Definition of a Pole in Complex Analysis

Equivalent in a neighborhood of z0, we can write

where for m = 1, we get a simple pole.

To give you a real life example, think of a streetlamp post, a fire hydrant, or any vertical bollard. It also happens to be a fixed point on the sidewalk where a dog might pause.

Photo by Maria Lin Kim on Unsplash

What Are Mathematical Residues???

This is a Laurent-series expansion of a complex function f(z).

If you know anything about series, it might look a bit similar to Taylor series to you. That’s because it is a generalization of such, and it includes both positive and negative powers k of (z−z0​), allowing it to represent functions with isolated singularities (like poles) within an annulus centered at z0.

Speaking of annulus, loyal readers of Math Games might remember the following geometry puzzle, which features a donut-like annulus.

A Geometry Puzzle with Two Concentric Circles ⭕🟡
How would you do it?medium.com

So the residue is the coefficient a_-1, which tells you exactly how the function behaves “around” the pole.