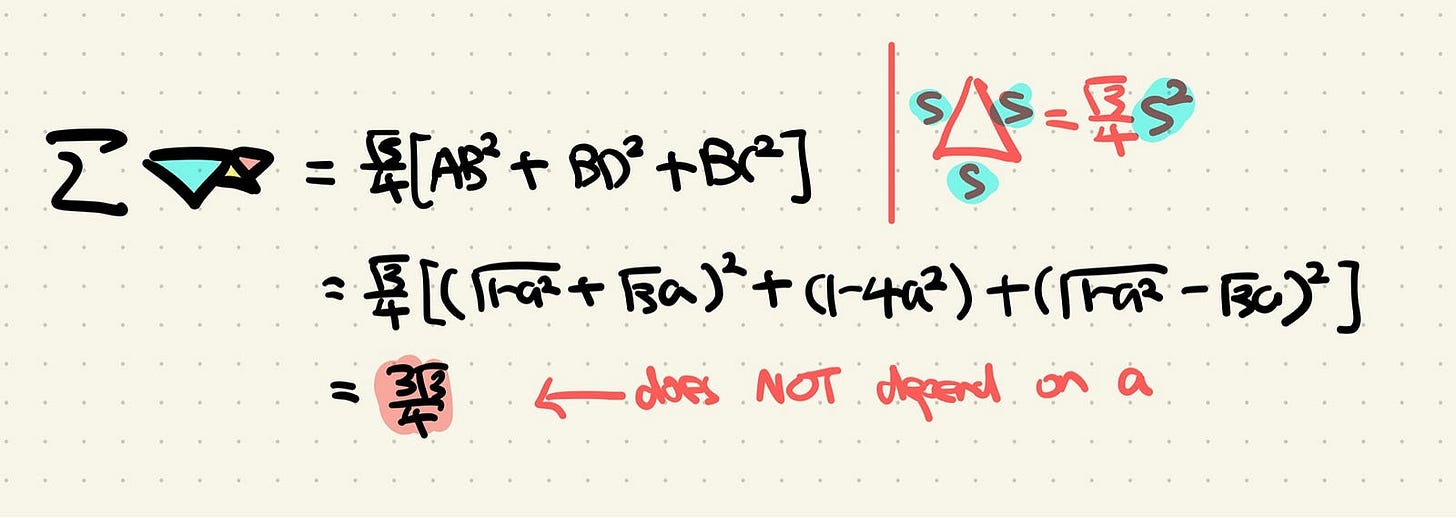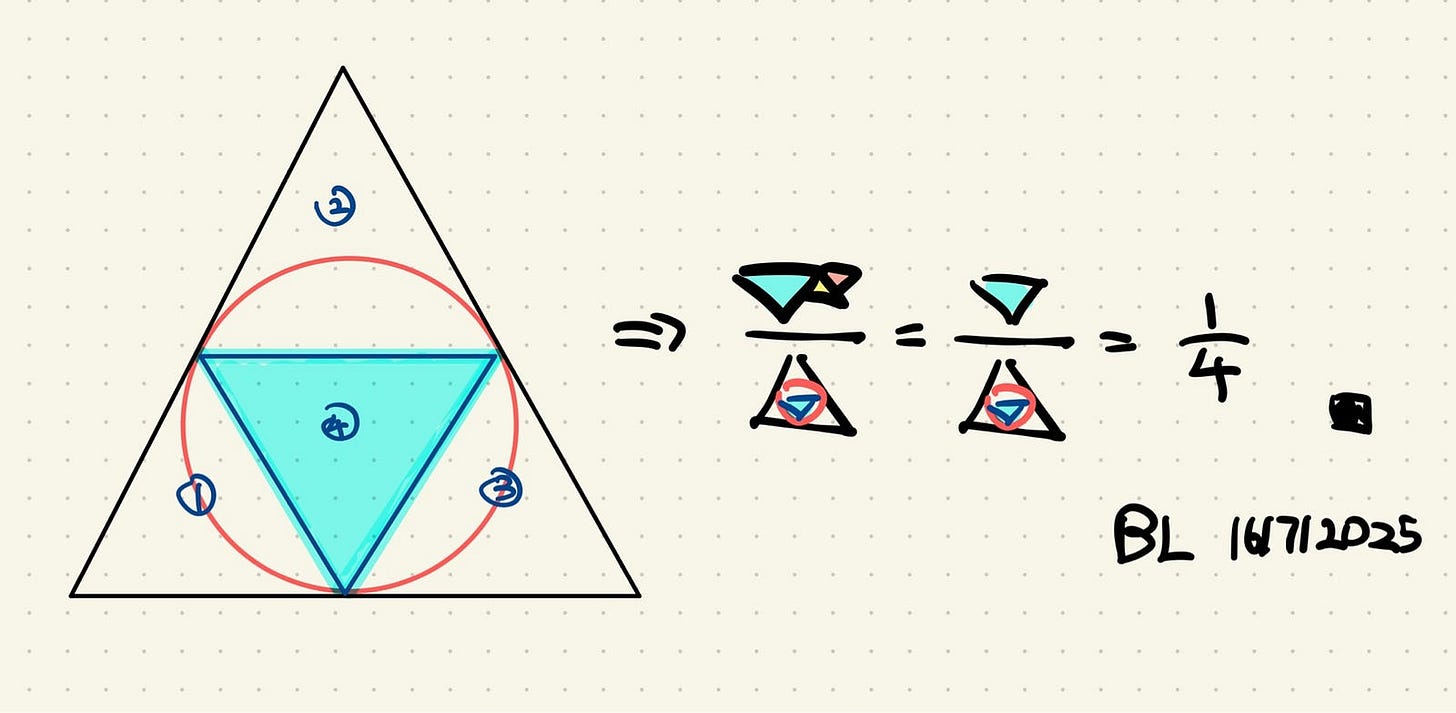Tell Me Why Meta Reasoning Works This Time
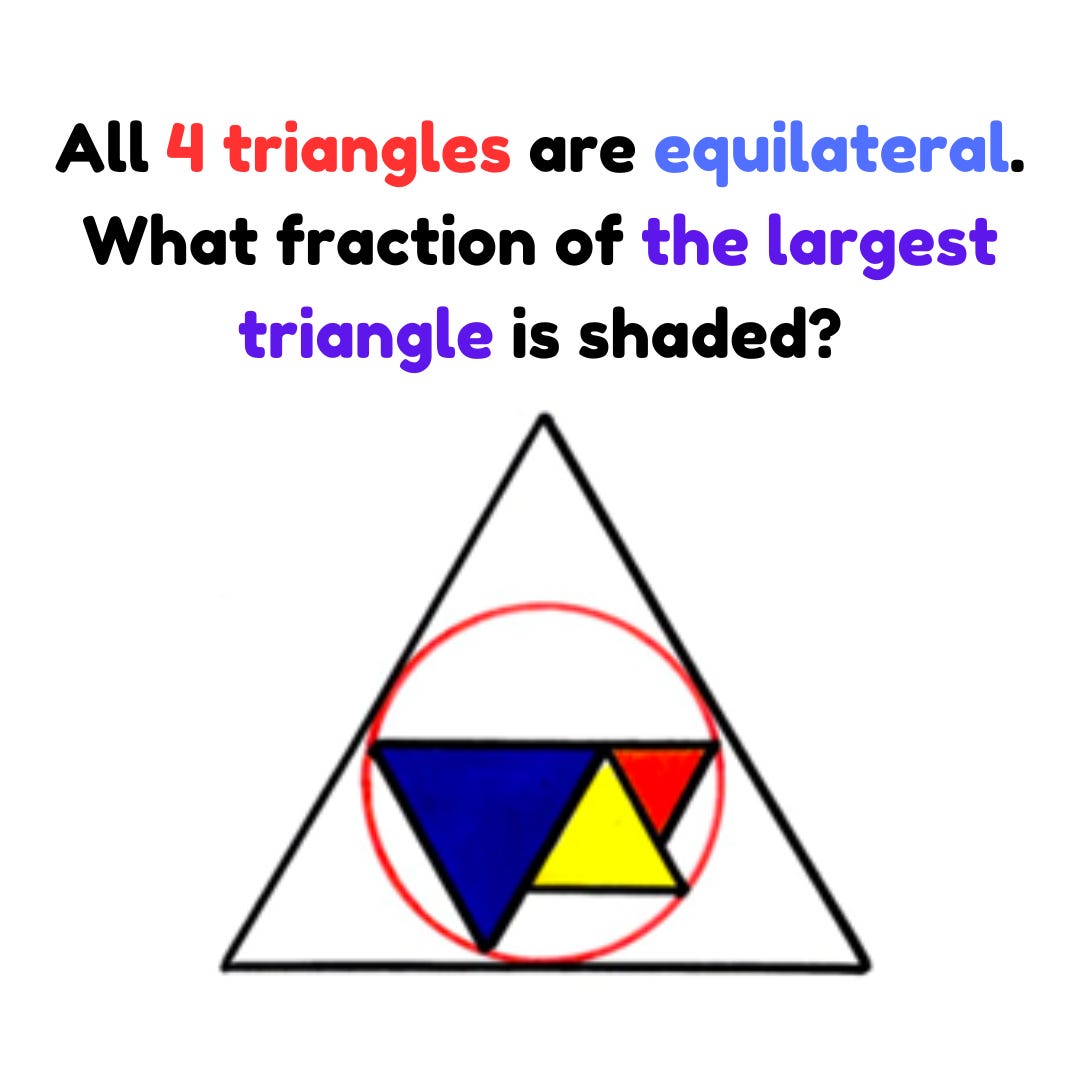
Catriona Agg’s Math Puzzle Challenge 6
Thanks to a fellow reader of Math Games Jonathan Lynn Harvey, I learnt that a ‘meta’ puzzle is a puzzle about a puzzle, akin to a metapoem being a poem about poetry per se.
In the context of geometry puzzles, a meta puzzle would involve finding out the hidden tricks within the setup of any given figure. More often than not, as many readers have pointed out in the last challenge, varying certain dimensions of the figures have no impact on the answer. And it’s through this one can arrive at the answer faster than the conventional way.
Of course, today’s puzzle is one of those meta puzzles. In fact, there are multiple configurations of how the 3 middle equilateral triangles can be positioned. This would make the solution way more elegant, albeit not mathematically rigorous.
So my challenge for you is not only to find the answer, but also proves to me concretely why the meta logic works for this specific puzzle.
Now without further ado, let’s dive in.
Solution
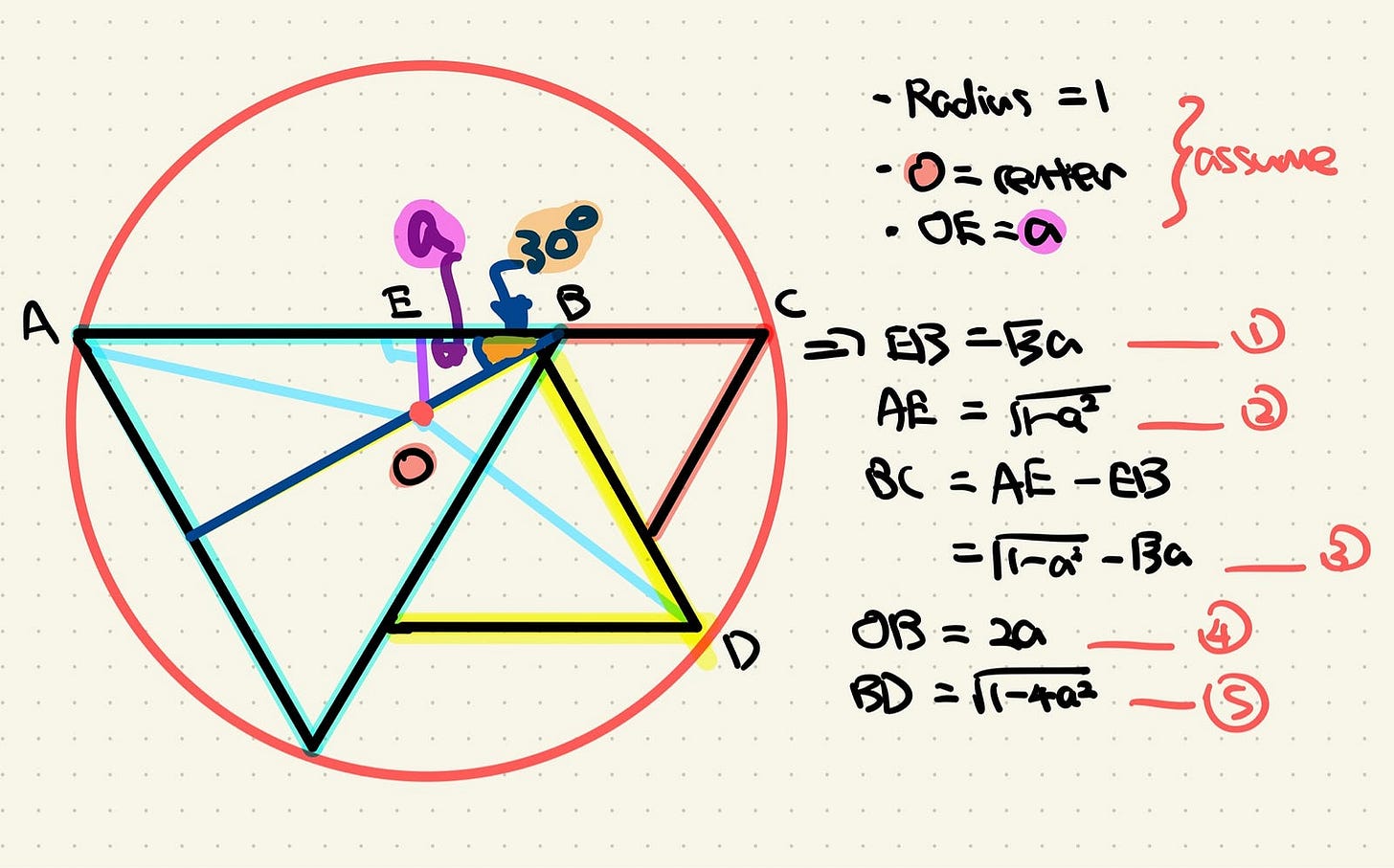
This is the setup for the solution.
We start by looking at the center of the circle, labelled O. The corners of the 3 triangles are labelled A, D and C. The point that touches the blue triangle and the red triangle is B. And the point that lies right above the center on the side of the blue triangle is E.
We’ve assumed a few things here. Firstly. we let the arbitrary radius of the circle be 1. It could have been anything else, but 1 usually allows for simpler arithmetic. We also let the length of OE be a. OE is of utmost significance here because as we can imagine, a varies as we change the shapes of the 3 triangles.
Try and visualize it in your head, if not feel free to take a look at this animation made by George Carey on X.
Then our task is to represent different segments on the diagram in terms of a.
EB can be found using trigonometric ratios.
AE is a result of the Pythagorean theorem.
BC is equivalent to AE − EB because O is the center of the circle and AE is essentially half of the chord.
OB is also a result of trigonometric ratios.
Finally BD is yet again a result of the Pythagorean theorem.
Originally I thought of explaining each step in more detail, but I think we should be able to work these out individually by just glancing over the diagram. Comment if you need some clarification!
The area of an arbitrary equilateral triangle of side s is √3/4s².
Then here we compute the total areas of the 3 equilateral triangles using the formula.
Fortunately for us, working through the algebra tells us the area is 3√3/4, which does not depend on a!
And this is the key! How? We shall see below.
Since the length of OE does not relate to the area of the 3 equilateral triangles, that means we can vary the configurations of the triangles as much as we want.
So we have justified our meta-approach and it should now be evident that the fraction is 1/4.
Illuminati sticker. 6 done. 308 more to go!
If you or anyone you know want to have online math lessons, please check out my tutoring site here. Thank you!
Barry — Online Maths tutor
40£/h : I offer tutoring in the following: GCSE Maths & Further Maths (All Exam Boards) A Level Maths & Further Maths…www.superprof.co.uk
Thank you so much for reading Math Games today, whether you are a math fan, an engineer, a lecturer, a banker, a scientist, or simply some curious soul who stumbled upon this article, I am happy that you stayed till the end. If you enjoyed this puzzle and believe in math education, please consider supporting here 🪙. It would help out my life and this blog a lot. Thanks!