Which Two Could Be The Sketch?
An Oxford MAT Problem
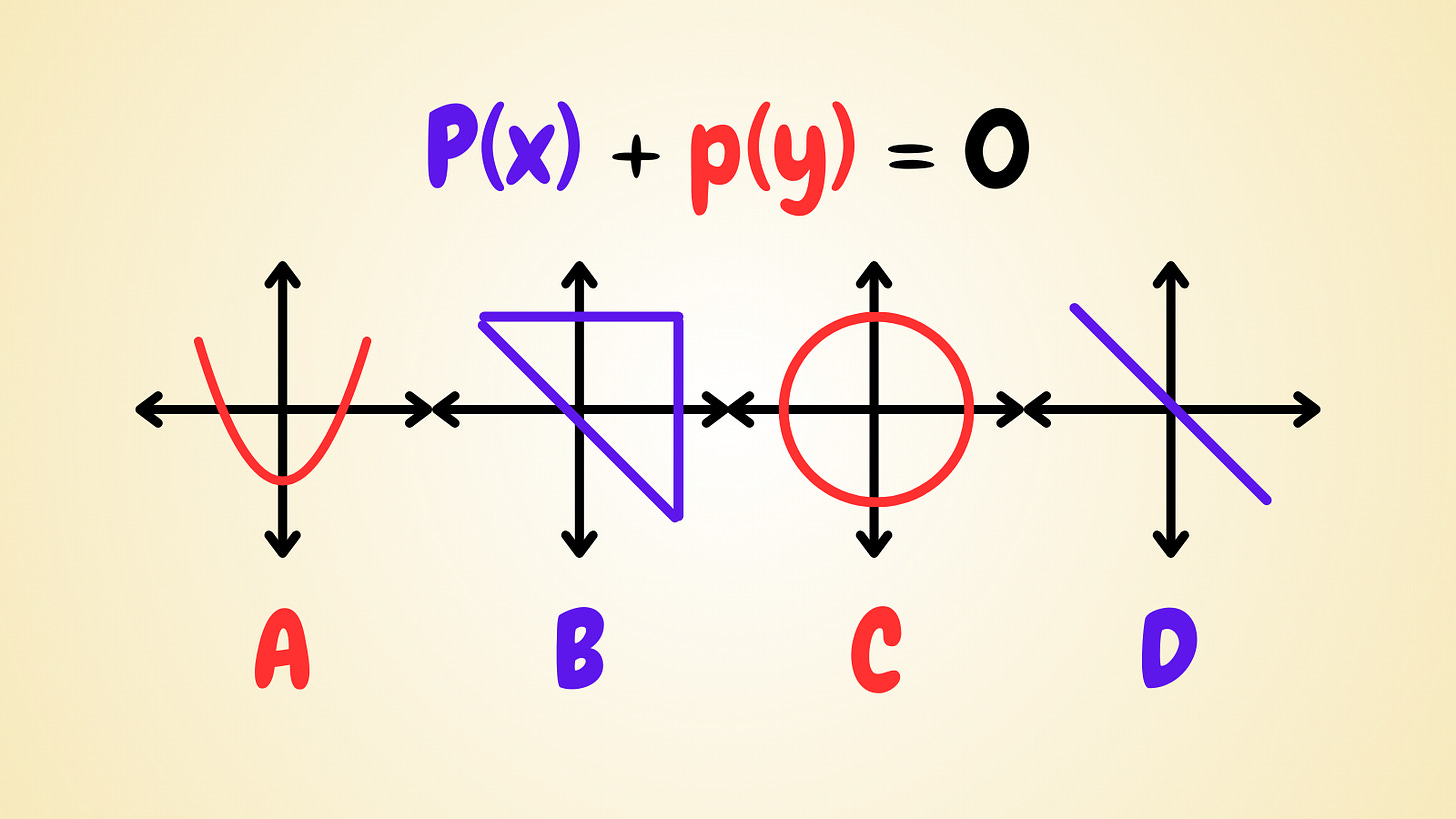
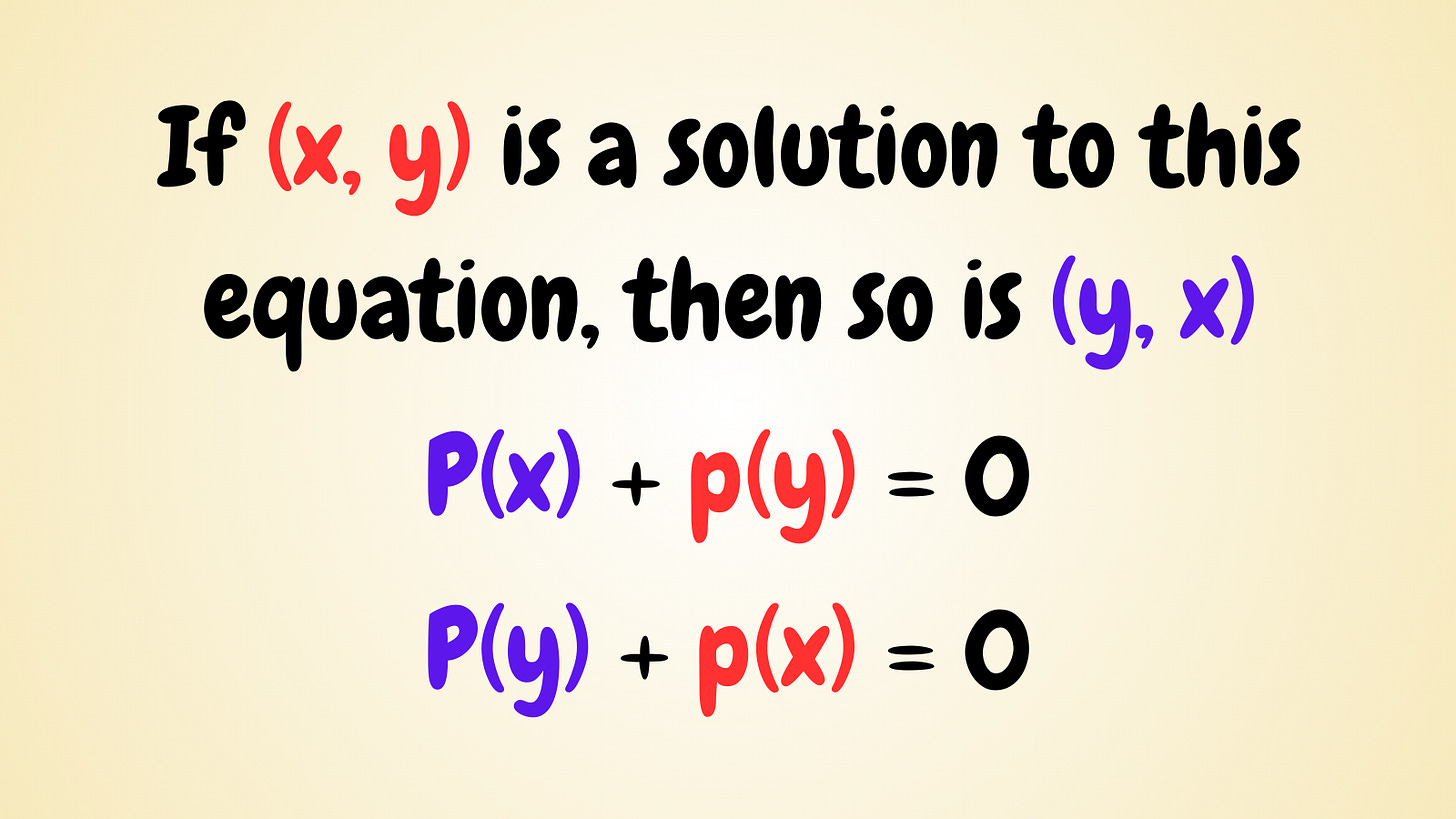Here p is some arbitrary polynomial. Now let’s say we have p(x) + p(y) = 0. Which two of the 4 graphs above could be the sketch of the equation p(x) + p(y) = 0 the polynomial p?
This very hard and interesting puzzle comes from the Oxford University’s math admission test. If you can get the answer, that means you have a very good understanding of functions and graphs, and perhaps you can attend Oxford University!
Anyway grab your pen and paper and give this a go, when you are ready scroll down for the solution.
If you’d like to support my work, please consider making a donation here.
Solution
The solution is actually just a few lines, so let’s take a look at this.
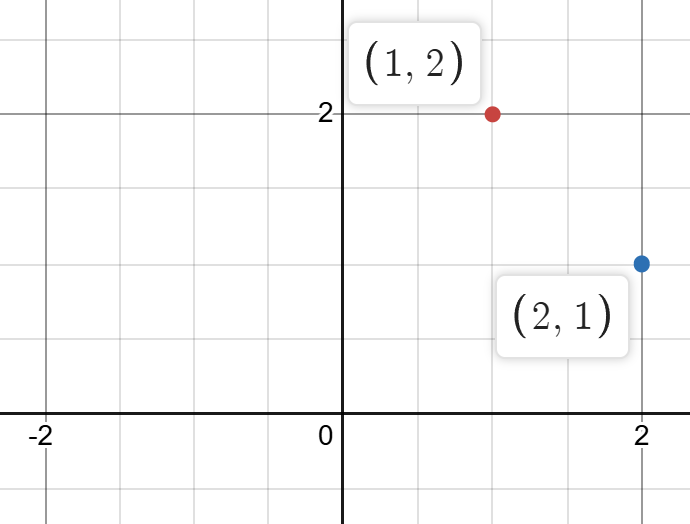
So for example, if the point (1, 2) exists on the curve, so does the point (2, 1).
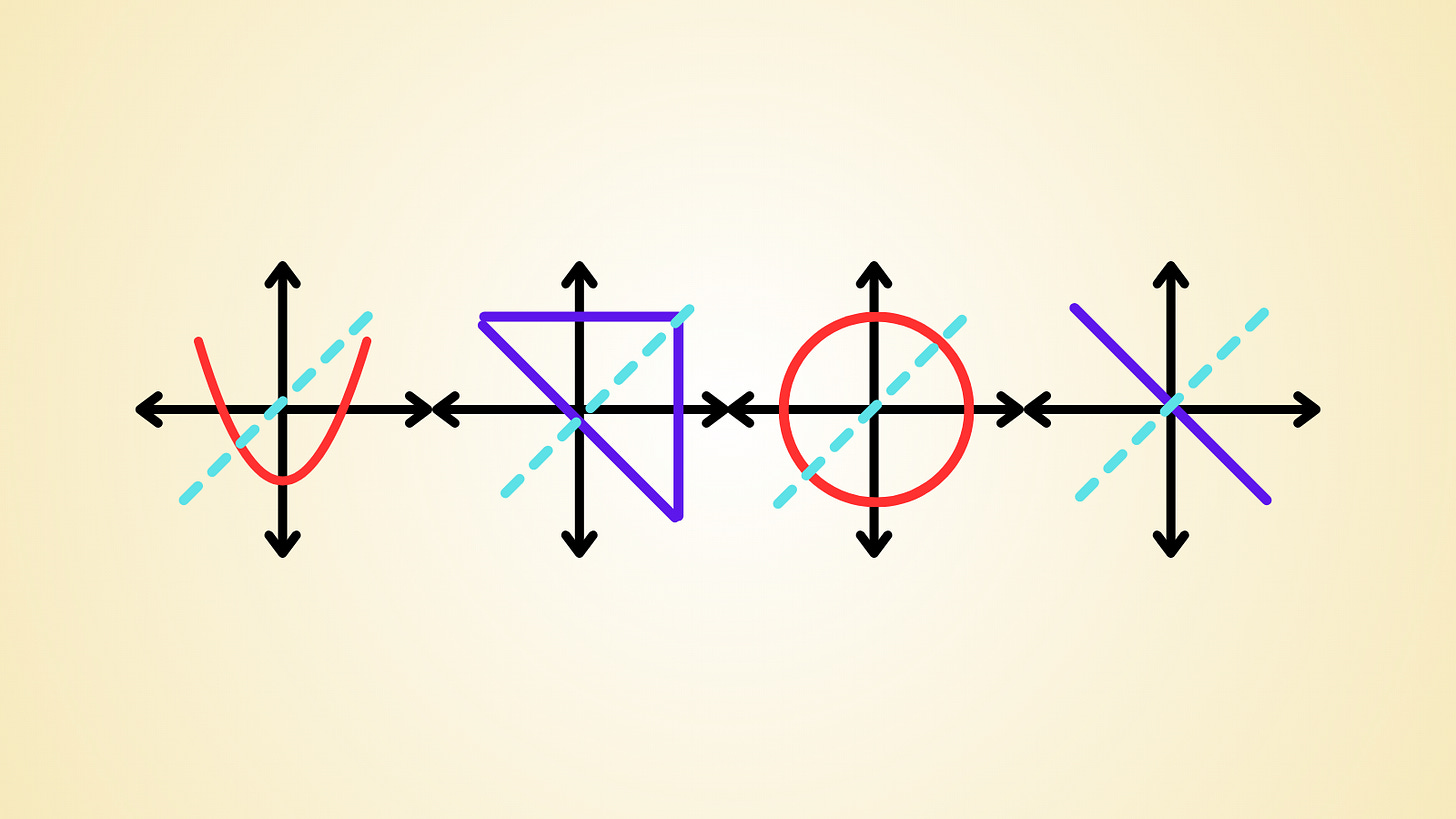
Now if we plot a few more points, we see that all those points are reflected across the line x = y. This means the graph must have reflectional symmetry in that line.
This means we have eliminated graph A. Now it looks like all of options B, C and D are possible. But given the title of the article, we know one of them is impossible.
Let’s check for certain that graphs C and D are possible.
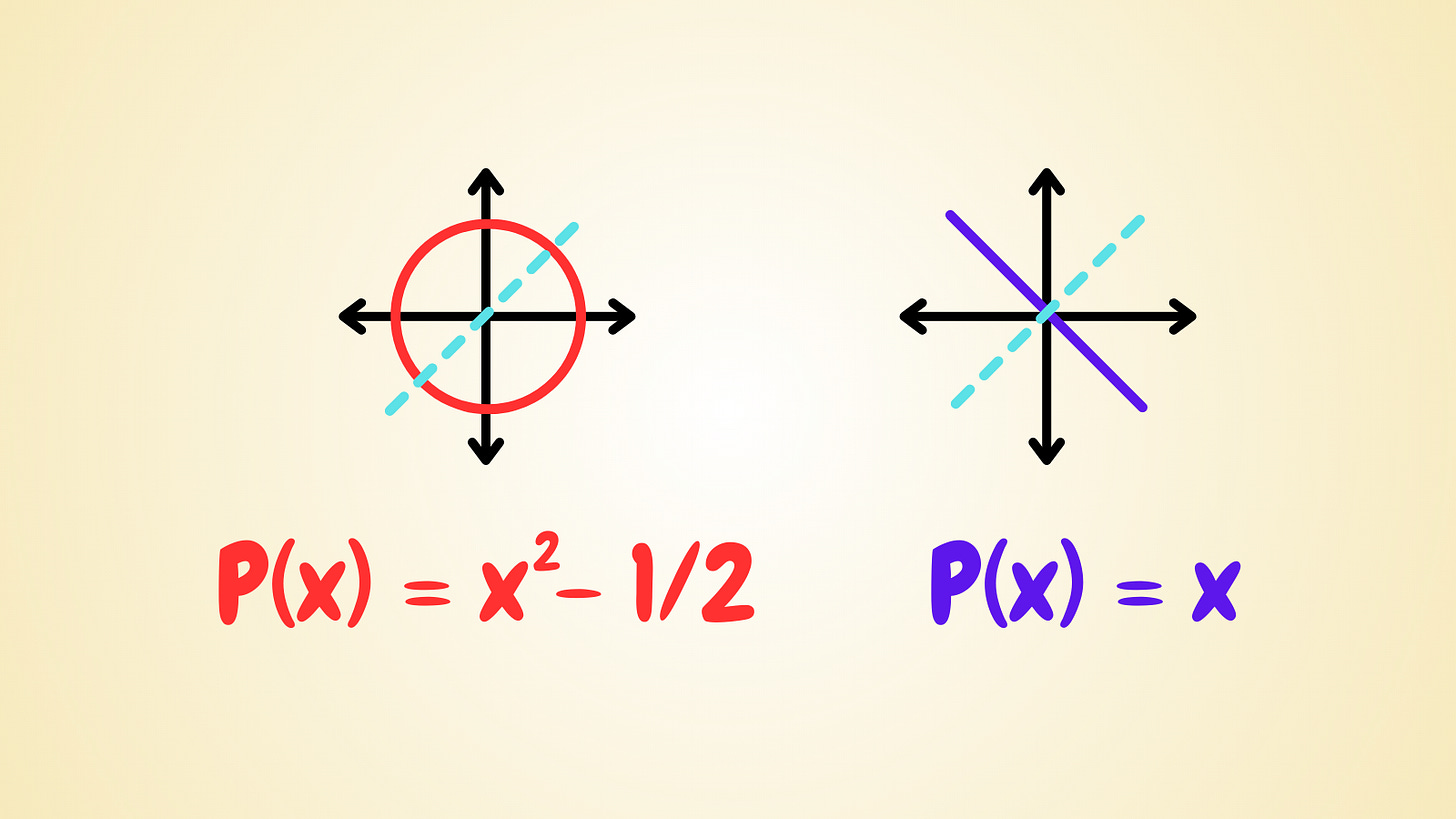
Now for the circle, if p(x) = x² -1/2, then p(x) + p(y) = x² + y² -1 = 0. So the equation is x² + y² = 1, which is the equation of a circle of radius 1 at the origin.
Equally for the straight line, if p(x) = x, then p(x) + p(y) = x + y = 0. So x = -y, which is exactly what the straight line is.
Now we know for certain that these two are possible sketches.
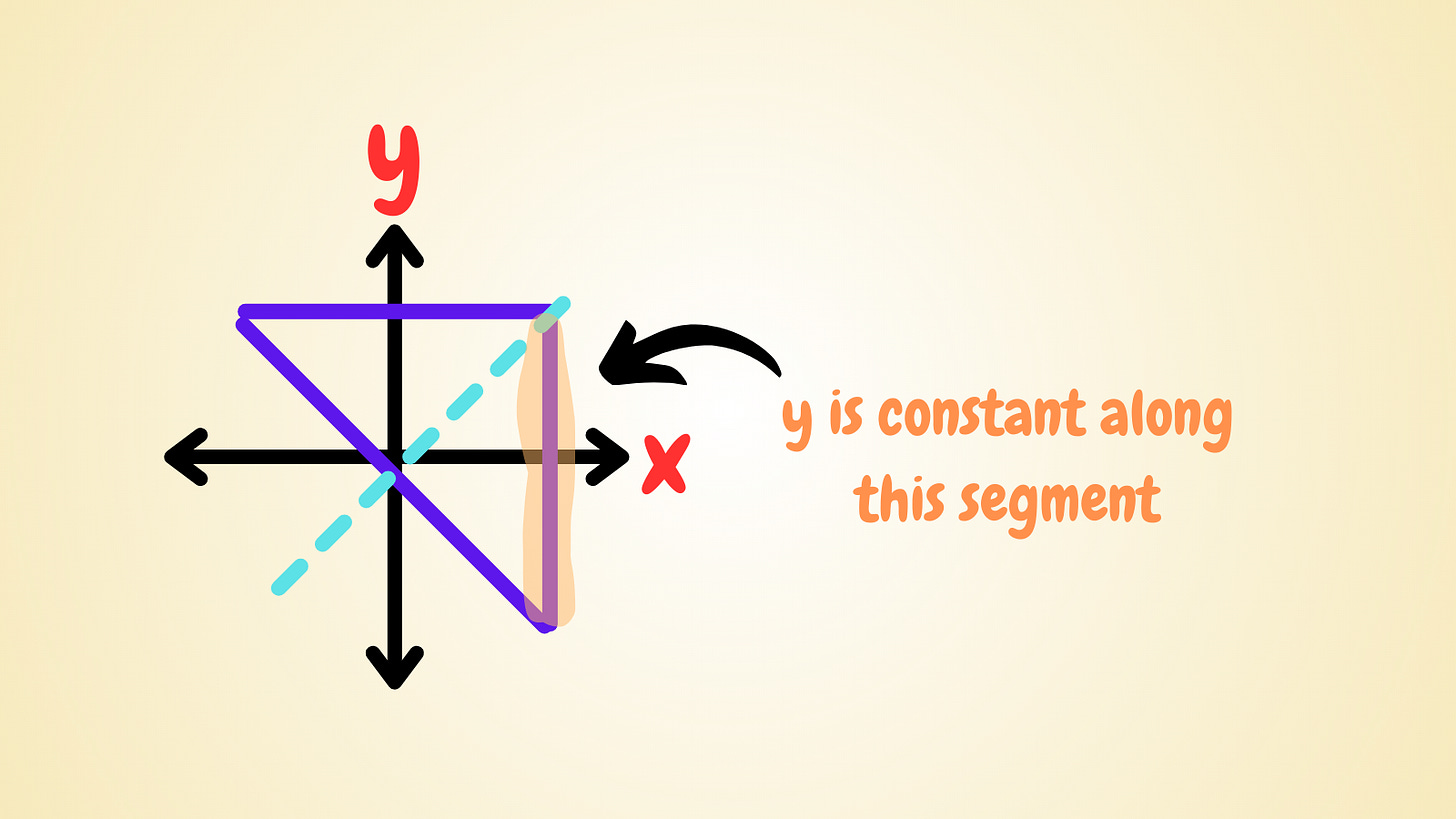
Perhaps to verify beyond certainty that only these two graphs are possible, we can show that graph B is impossible.
For B, look at the part of the sketch with y constant. Along this line segment, p(x) + p(y) = 0 and p(y) is a constant. But if this polynomial is zero in some interval, it must be zero for all x, so p(x) must be constant! But then either all points should be in the sketch (if the constant is zero) or none should (otherwise).
That means this sketch is neither, and therefore impossible.
So the only two graphs are C and D. And that’s our answer. How amazing!
If you or anyone you know want to have online math lessons, please check out my tutoring site here. Thank you!
Barry Leung
Math tutoringonlinemathtutor.carrd.co
Thank you so much for reading Math Games today, whether you are a math fan, an engineer, a lecturer, a banker, a scientist, or simply some curious soul who stumbled upon this article, I am happy that you stayed till the end. If you enjoyed this Oxford math puzzle and believe in math education, please consider supporting here 🪙.
