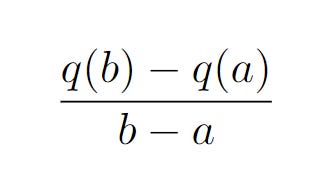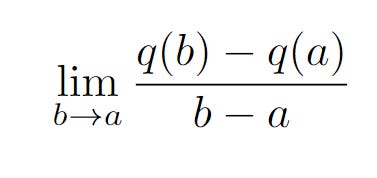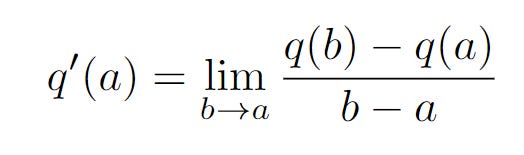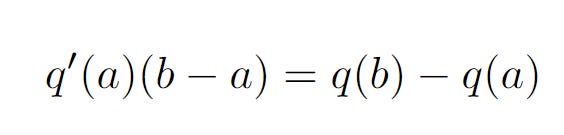Why Does The Definite Integral Equal Area?

The Fundamental Theorem Of Calculus

---

Photo by Monstera

If you have taken high school calculus, you probably have computed a definite integral to find the area under a curve. But have you ever thought about the relation between the two, in particular, why the value of the definite integral gives us the area under the curve. Well, I am glad you have stumbled upon this article because I am about to guide you through the thought process behind it.

Without further ado, let’s dive in!

---

To start with, recall the idea of the derivative. In a nutshell, it’s bringing two points on a curve closer and closer together and finding the gradient at that particular point.

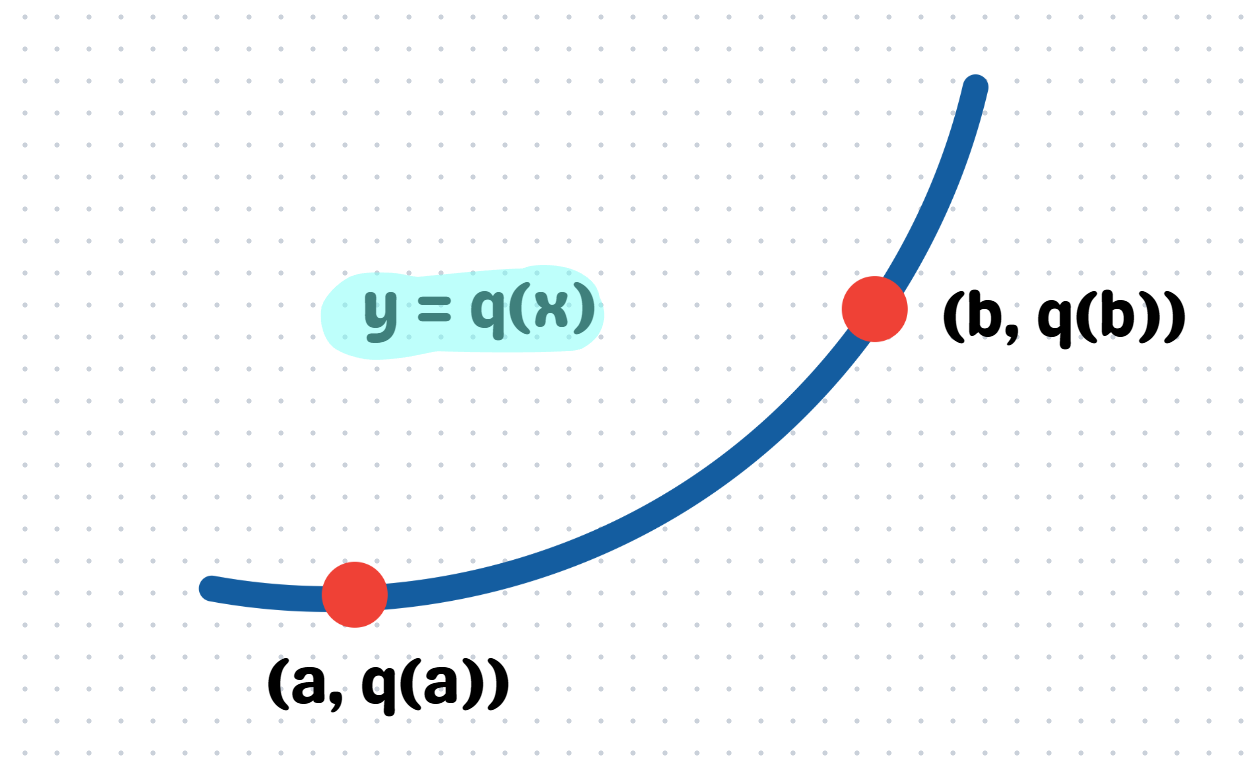
Now consider a function y = q(x). We then pick two arbitrary points on the curve, (a, q(a)) and (b, q(b)).

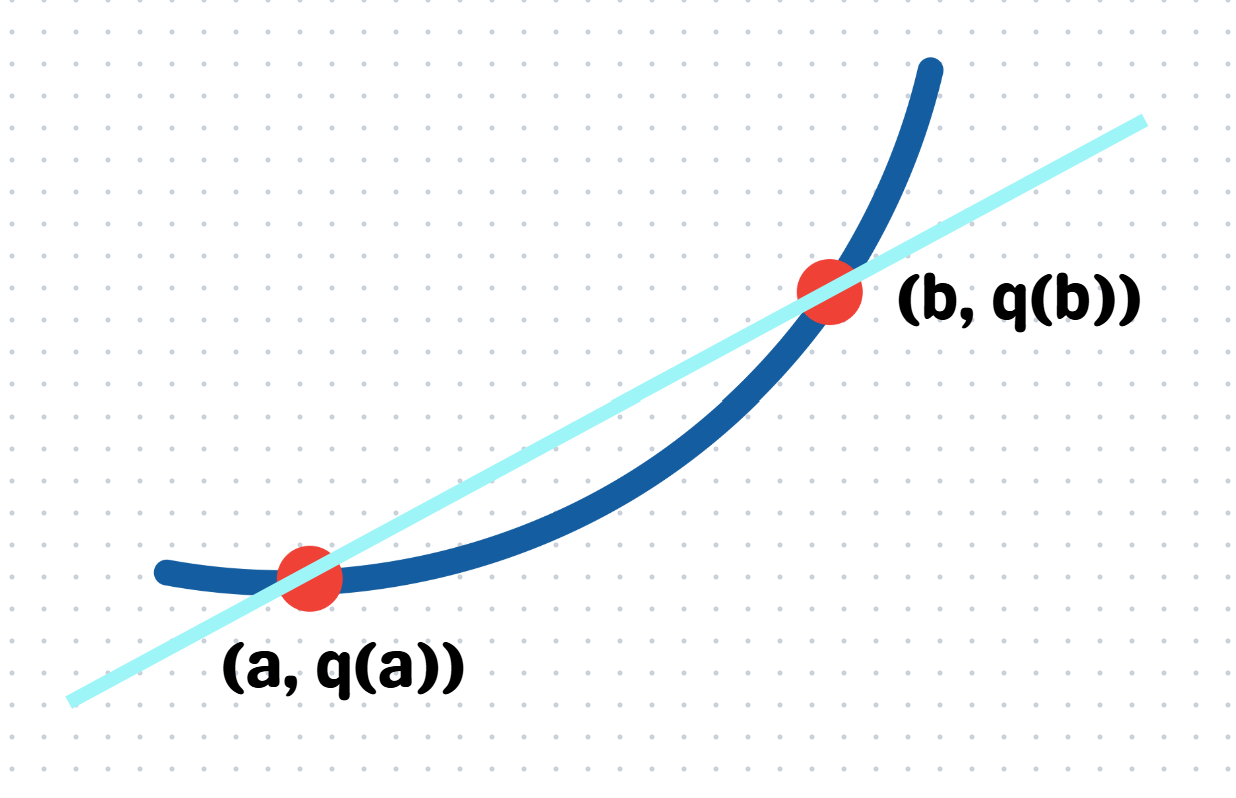
If we want to find the gradient of these two points, we have

But this expression gives us the slope of two points, a and b. We are interested in finding the gradient at one point, which is a. We will have the following limit.

This is equivalent to the idea behind the derivative, bringing point b closer and closer to a. Which means, this is the derivative of the function q(x) at a.

Therefore, we have

However, when b is really close to a, we can get rid of our limit notation and say

keep this formula in mind

Let’s keep this formula in mind for now.